Progressive Lens design is a complex problem. As described in our PAL Anatomy article, there are a large number of lens details to optimize and trade-off. Further, it is not even clear how one can change such structural features to get the desired result.
SimuLens
SimuLens performs a realistic simulation of a spectacle lens in use. The lens is to be described by arbitrary sets of points describing the front and back surfaces (e.g. generator points-files), and a refractive index. The eye position relative to the points is computed based on fitting parameters.
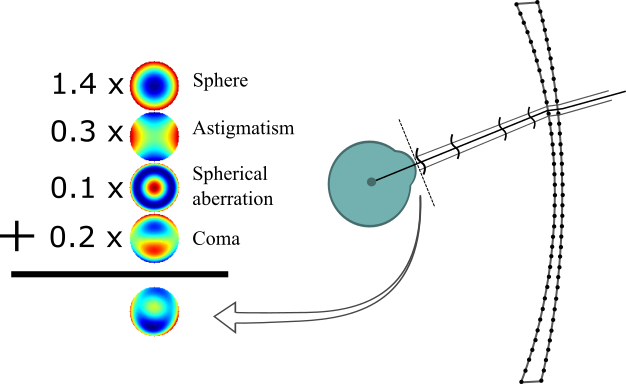
Zernike Polynomials
Truncated expansions such as Zernike polynomials provide a powerful approach for describing wavefront data. However, many simple calculations with data in this form can require significant computational effort. Important examples include recentering, renormalizing, and translating the wavefront data. This paper describes a technique whereby these operations and many others can be performed with a simple matrix approach using monomials. The technique may be applied to other expansions by reordering the data and applying transformations. The key is the use of the vectorization operator to convert data between vector and matrix descriptions. With this conversion, one-dimensional polynomial techniques may be employed to perform separable operations. Examples are also given for differentiation and integration of wavefronts.
Keith Dillon, “Bilinear wavefront transformation,” J. Opt. Soc. Am. A 26, 1839-1846 (2009) (pdf)
