Progressive Lens design is a complex problem. As described in our PAL Anatomy article, there are a large number of lens details to optimize and trade-off. Further, it is not even clear how one can change such structural features to get the desired result.
The typical approach to lens design is depicted below. The lens designer controls a lens generator of some kind, which provides the ability to produce a range of variations of a lens. When a lens is produced, it is analyzed and tested, and the results are used to adjust the inputs in order to hopefully generate a better lens. Typically a large number of adjustments and settings are preset to fixed values to make the problem manageable.
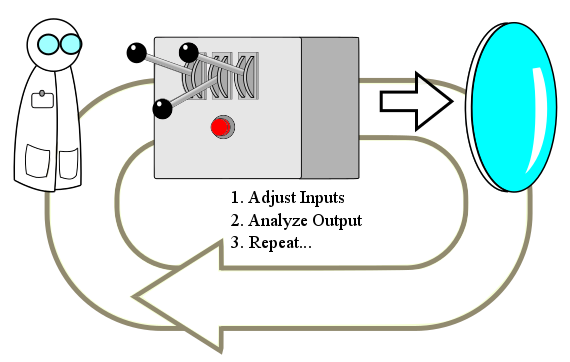
The loop defines an optimization process, the lens is meant to be improved at each iteration of the loop until it reaches an “optimal” result.
There are multiple problems with this typical approach…
- There are a very large number of potential adjustment combinations to try.
- The resulting design tailored to particular Rx.
- The resulting design is tailored either to a specific use, or broadly usable but ideal for no specific use.
Lens Optimization
Optimization is a very broad term. When a vendor says their lens design has been optimized for a particular customer, this could mean very little in practice; only that something about the lens was changed to improve the result. Perhaps they did nothing more than tweak the add power based on the prescribed sphere. If fact, it is most commonly the case that the value being optimized is the sphere and the point of ”optimization” is merely to correct for error that their own crude approximation had previously introduced.
To understand what is missing and why vendors take such shortcuts, consider that a progressive lens can have varying sphere and cylinder powers at each point on the lens, not to mention high-order variations as well. For a points-file with half-millimeter spacing, this amounts to tens of thousands of values to be decided. In this form, there are far too many “levers” to adjust to make a lens with desirable properties.
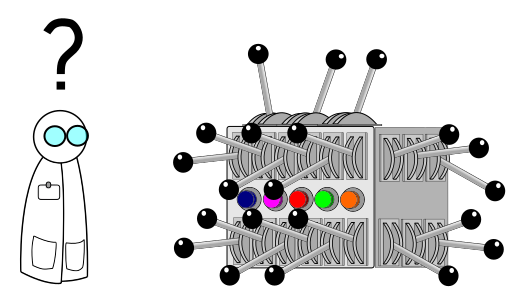
The most common technique is to describe the lens with a parametric set of equations, typically splines. This reduces those thousands of variables describing the surface down to a handful, but also severely restricts the freedom to optimize the surface.
The next problem is deciding how to adjust these variables. The overwhelmingly-common approach is to package them up using fudge factors with no physical meaning. Most commonly, an average error between a desired lens performance and measured lens performance is computed over all points. Then the optimization problem is to minimize this average error.
This sounds reasonable, but treats error in important regions, such as the distance-viewing zone, on an equal footing with less important regions.
This is commonly addressed with fudge factors known as “weights” which scale the error at different points on the lens in order to enforce better quality in certain regions (e.g. the distance zone) and the expense of other regions (e.g. swim zones). The problem is these weights lack physical meaning, one must simply follow a process of “guess-and-check” to see what values work best.
This design process can best be described as an art rather than a science.
There is no mathematical basis for arguing the “optimal” lens produced with a set of designer-chosen weights is really optimal for vision anymore. Optimal in such context, to be clear, should mean the least distortion or highest visual quality possible. And with an “art” process requiring designer skill and interaction, this is practically impossible.
Every Eye is Unique
The basis for this (and the next) problem might be termed the “Designer-in-the-loop” shortcoming. Utilizing the typical and non-intuitive process by which lens design is usually performed requires both a lens designer highly skilled in the art of Lens Design.
Is not practical to “optimize” all prescriptions via a process which requires such hands-on interaction. The approach used instead is to produce a design for plano prescriptions, and adjust this design to serve different prescriptions using a so-called composite surface approach.
Composite surfaces are the result of combining a height map representing optimized for one situation with another height map (often spherocylindrical) to provide a result that approximately addresses a different situation.
Such a design is no longer optimal due to the nonlinearity of refractive optics.
The composite surface is only an approximation. This is one example of the kind of error introduced by the lens designer, that they often subsequently apply a much-touted ”optimization” technique to correct.
The Lens Market(s)
A related problem is the fact that each design manually “optimized” must be tailored to a certain market. As depicted in our Market Segmentation Post, lens designers typically break the market down into a handful of segments.
Every market may be more accurately be viewed and consisting of many more smaller markets, differentiated by variations in the ideal lens specifications.
Lens Engineering
Now we will describe the scientific approach to lens design employed by FormuLens, and how this is applied to FormuLens products.
FormuLens provides a control of lens performance at the intuitive level of design requirements. As depicted in the Figure below, Lens Designers (or anyone else) is presented with a small set of controls, depicted by the few external levers. These controls allow the designer to provide meaningful performance targets for the lens, and free the designer from the need to become actively involved and an expert at how the local details of the lens surface relate to the desired outcome.
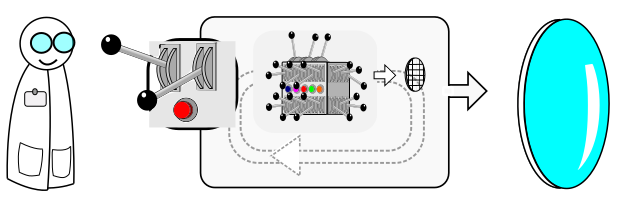
The optimization loop is now an internal process which does not require designer interaction. It has the following goal: produce the lens with the highest visual performance which achieves the input parameters.
Visual quality is based on the full high order wavefront estimate of gaze through the lens at each point on the pointsfile. This is all computed internally via exacting optical simulation.
We can break this technology into three components:
- Powerful and Intelligent optimization algorithms.
- Thorough optical simulation, including high order (see SimuLens).
- Interface to user/design expertise/art.
